はじめに
ニューラルネットの挙動を理解する:全結合層と活性化関数による変換での可視化が魅力的だったので、Julia の Flux.jl で同様のことをやってみました
問題設定
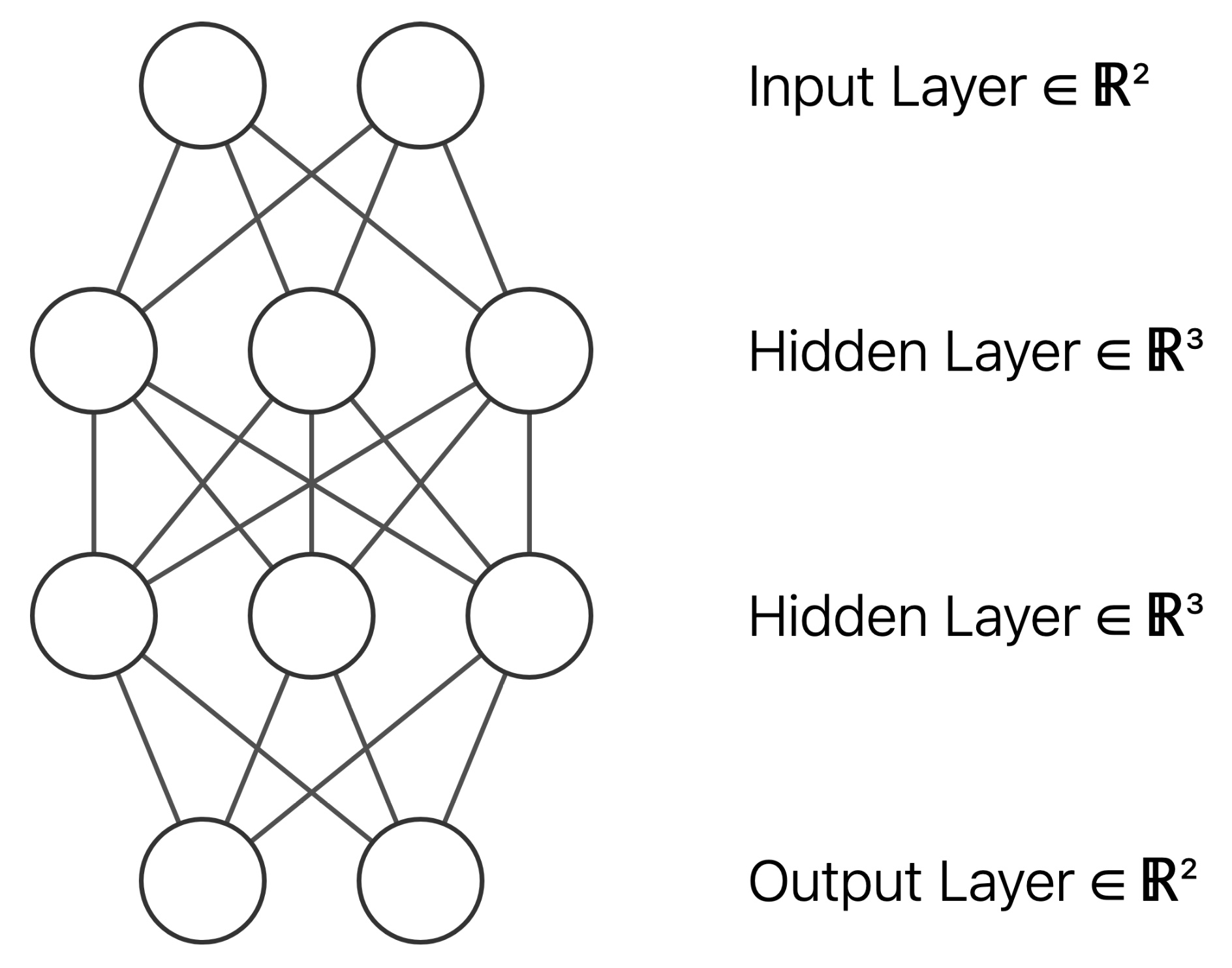
- 3層のニューラルネットワークで下図のデータを2値分類
- ネットワークの構造
TODO: アフィン変換をする隠れ層が入力層の直後に追加で入るにも関わらず、図に描き忘れているので修正
Julia での実装
- パッケージのインポート
using Flux using LinearAlgebra using Plots using ProgressMeter - 訓練用の入力
# 円状に点を作成 circle_coords(r_min, r_max, r_size, θ_size) = [ r .* (sin(θ), cos(θ)) for θ in range(0, 2π, length=θ_size) for r in range(r_min, r_max, length=r_size) ] N = 30 x_coords = [ circle_coords(1e-3, 1 / 3, N, N), circle_coords(2 / 3, 1, N, N) ] coords2mat(xs) = hcat([[xs[n]...,] for n in axes(xs, 1)]...) x_train = (coords2mat ∘ vcat)(x_coords...); - 入力に対応する教師ラベルを生成して
🚫
Post not found と結合
y_train = (coords2mat ∘ vcat)( [(1, 0) for _ in 1:N^2], [(0, 1) for _ in 1:N^2] ); data = [(x_train, y_train)]; - ニューラルネットワークを学習
# 訓練対象のモデル作成 model = Chain( Dense(2 => 3), Dense(3 => 3, relu), Dense(3 => 3, relu), Dense(3 => 2), softmax ) # モデルの学習 epoch_num = 50_000; params = Flux.params(model); regular_rate = 0.01; loss(x, y) = Flux.crossentropy(model(x), y) + regular_rate * norm(params); opt = Descent() @showprogress "Epoch of training: " for epoch in 1:epoch_num Flux.train!(loss, params, data, opt) end - 格子点
function grid_coords(x_coords) x_mat = coords2mat(x_coords) x₁_min, x₁_max = round.([minimum(x_mat[1, :]), maximum(x_mat[1, :])]) x₂_min, x₂_max = round.([minimum(x_mat[2, :]), maximum(x_mat[2, :])]) [ Float64.((i, j)) for i in range(x₁_min, x₁_max, length=100) for j in range(x₂_min, x₂_max, length=100) ] end -
🚫
Post not found , 🚫
Post not found を線形補間する関数の定義
また,中間層の出力は最初の2次元のみ表示に用いる# リストの隣接する要素の平均値をその要素間に挿入 insert_lerp(xs) = let xs_lerp = [ [ (xs[n][i] .+ xs[n+1][i]) ./ 2 for i in axes(xs[n], 1) ] for n in axes(xs, 1)[1:end-1] ] [ n % 2 == 0 ? xs_lerp[div(n, 2)] : xs[div(n, 2)+1] for n in 1:2size(xs, 1)-1 ] end # GIF生成のためのフレームを作成 # フレーム数はおよそ 2^log2_expansion_rate 倍となる function create_frames(x_coords, log2_expansion_rate=6) x_mat = coords2mat(x_coords) anim_x = [x_coords] for layer_depth in 1:length(model) mat2coords(xs) = [(xs[:, j]...,) for j in axes(xs, 2)] y = model[1:layer_depth](x_mat)[1:2, :] # 最初の2次元をプロットに使用 y_coords = mat2coords(y) anim_x = [anim_x..., y_coords] end foldl(∘, repeat([insert_lerp], log2_expansion_rate))(anim_x) end - Plots の
@gifマクロでアニメーションを生成# 訓練結果のブロット x_plot = [ circle_coords(1e-3, 1 / 3, N, N), circle_coords(2 / 3, 1, N, 5N) ]; anim_xplot = create_frames.(x_plot); # 格子点のプロット anim_xgrid = (create_frames ∘ grid_coords ∘ vcat)(x_plot...); # プロット用の点をまとめる anim_plots = zip(anim_xplot..., anim_xgrid); gif_prog = Progress(length(anim_plots), desc="Render GIF: "); @gif for (x₁, x₂, xgrid) in anim_plots plot() plot!(xgrid, seriestype=:scatter, mc=:gray, ma=0.3, ms=2, label="grid") plot!(x₁, seriestype=:scatter, mc=:red, ma=0.3, ms=6, label="label1") plot!(x₂, seriestype=:scatter, mc=:blue, ma=0.3, ms=6, label="label2") next!(gif_prog) end
ソースコード全体
using Flux
using LinearAlgebra
using Plots
using ProgressMeter
coords2mat(xs) = hcat([[xs[n]...,] for n in axes(xs, 1)]...)
mat2coords(xs) = [(xs[:, j]...,) for j in axes(xs, 2)]
insert_lerp(xs) =
let xs_lerp = [
[
(xs[n][i] .+ xs[n+1][i]) ./ 2
for i in axes(xs[n], 1)
]
for n in axes(xs, 1)[1:end-1]
]
[
n % 2 == 0 ? xs_lerp[div(n, 2)] : xs[div(n, 2)+1]
for n in 1:2size(xs, 1)-1
]
end
function create_frames(x_coords, log2_expansion_rate=6)
x_mat = coords2mat(x_coords)
anim_x = [x_coords]
for layer_depth in 1:length(model)
y = model[1:layer_depth](x_mat)[1:2, :]
y_coords = mat2coords(y)
anim_x = [anim_x..., y_coords]
end
foldl(∘, repeat([insert_lerp], log2_expansion_rate))(anim_x)
end
# 格子点を作成
function grid_coords(x_coords)
x_mat = coords2mat(x_coords)
x₁_min, x₁_max = round.([minimum(x_mat[1, :]), maximum(x_mat[1, :])])
x₂_min, x₂_max = round.([minimum(x_mat[2, :]), maximum(x_mat[2, :])])
[
Float64.((i, j))
for i in range(x₁_min, x₁_max, length=100)
for j in range(x₂_min, x₂_max, length=100)
]
end
# 円状に点を作成
circle_coords(r_min, r_max, r_size, θ_size) = [
r .* (sin(θ), cos(θ))
for θ in range(0, 2π, length=θ_size)
for r in range(r_min, r_max, length=r_size)
]
# 訓練データの作詞
N = 30
x_coords = [
circle_coords(1e-3, 1 / 3, N, N),
circle_coords(2 / 3, 1, N, N)
]
x_train = (coords2mat ∘ vcat)(x_coords...);
y_train = (coords2mat ∘ vcat)(
[(1, 0) for _ in 1:N^2],
[(0, 1) for _ in 1:N^2]
);
data = [(x_train, y_train)];
# 訓練対象のモデル作成
model = Chain(
Dense(2 => 3),
Dense(3 => 3, relu),
Dense(3 => 3, relu),
Dense(3 => 2),
softmax
)
# モデルの学習
epoch_num = 50_000;
params = Flux.params(model);
regular_rate = 0.01;
loss(x, y) = Flux.crossentropy(model(x), y) + regular_rate * norm(params);
opt = Descent()
@showprogress "Epoch of training: " for epoch in 1:epoch_num
Flux.train!(loss, params, data, opt)
end
# 訓練結果のブロット
x_plot = [
circle_coords(1e-3, 1 / 3, N, N),
circle_coords(2 / 3, 1, N, 5N)
];
anim_xplot = create_frames.(x_plot);
anim_xgrid = (create_frames ∘ grid_coords ∘ vcat)(x_plot...);
anim_plots = zip(anim_xplot..., anim_xgrid);
gif_prog = Progress(length(anim_plots), desc="Render GIF: ");
@gif for (x₁, x₂, xgrid) in anim_plots
plot()
plot!(xgrid, seriestype=:scatter, mc=:gray, ma=0.3, ms=2, label="grid")
plot!(x₁, seriestype=:scatter, mc=:red, ma=0.3, ms=6, label="label1")
plot!(x₂, seriestype=:scatter, mc=:blue, ma=0.3, ms=6, label="label2")
next!(gif_prog)
end実行結果
ネットワークは 2 → 3 → 3 (活性化関数) → 3 (活性化関数) → 2 → softmax で構成しています
ちなみに,サムネで使用したネットワークの構造は 2 → 3 → 3 (relu) → 3 (tanh) → 2 → softmax で活性化関数が少し異なります
Tanh
3次元空間をうまく捻じ曲げることで,2値分類を行えています
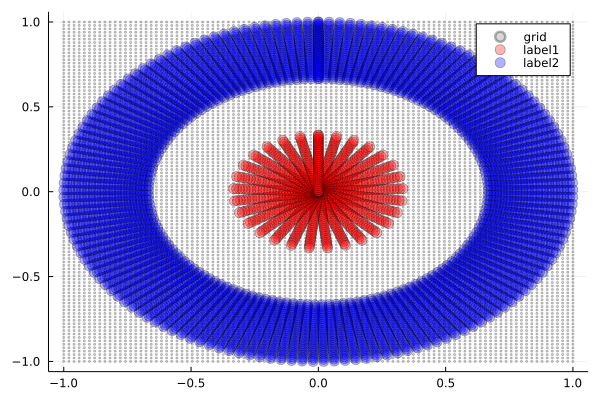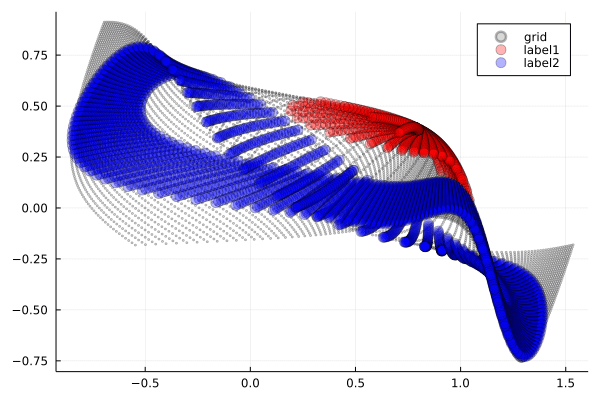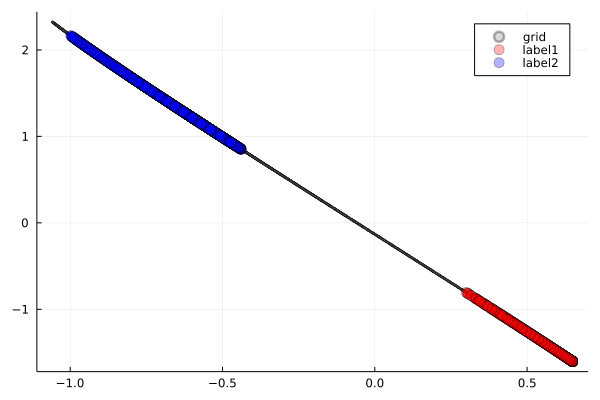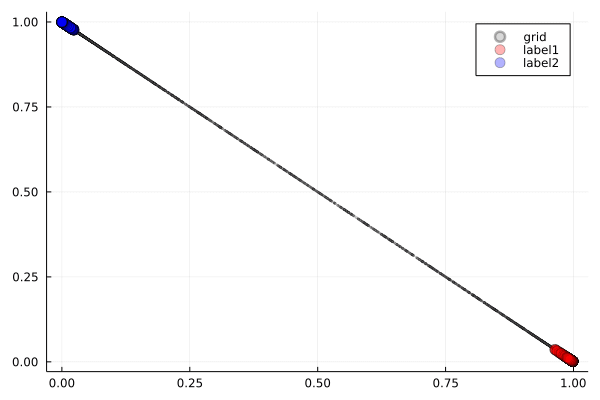
ReLU
2次元入力を3次元空間の中で折り畳むことで,2値分類を実現している様子が見て取れます

GeLU
GeLU は ReLU の亜種の一つです.ReLU との違いを見てみましょう
ReLU と同様に入力を折り畳む様子が見て取れますが,こちらはより滑らかに折り畳んでいます

まとめ
以上が Julia によるニューラルネットワークの可視化についての紹介でした
このような可視化を浅層ネットワークのダイナミクス解析に利用した例があれば,興味があるので教えてくださればと思います

 Nov’s AI Blog
Nov’s AI Blog